Vergabeblog
"Hier lesen Sie es zuerst"Faktencheck Vergabemathematik: Der Mythos der 50 %-Gewichtung (VK Lüneburg, Beschl. v. 05.09.2023 – VgK-20/2023)

Laut einer sehr weit verbreiteten Ansicht erzwingt die Einfache Richtwertmethode ganz offensichtlich eine 50 %-Gewichtung zwischen Leistung und Preis. So hat nun auch die VK Lüneburg ihren Beschluss unter Bezugnahme auf mehrere Vergaberechtskommentare begründet. Aber so offensichtlich, wie man meinen könnte, ist es nicht – Gehen wir der Behauptung also einmal auf den Grund:
Sachverhalt
Der AG schreibt die Lieferung und Einrichtung von Multifunktionsprintern im Mietmodell aus. Als Zuschlagsmethode wurde die Einfache Richtwertmethode – also das Preis-Leistungsverhältnis im strengen Sinn – verwendet.
Ein Bieter beschwert sich wie folgt:
„Außerdem verstoße die Ausschreibung gegen § 58bs. 3 VgV, da es vom Antragsgegner versäumt wurde, in der Auftragsbekanntmachung bzw. in den Vergabeunterlagen die Gewichtung der einzelnen Zuschlagskriterien mitzuteilen.“
Die Vergabekammer schließt sich diesem Argument nicht an, sondern begründet:
„Bereits im Jahre 2003 wurde mit der UfAB III die ‚Einfache Richtwertmethode‘ (Z = L : P) eingeführt. L steht für die tatsächlich erreichten Leistungspunkte. P steht für den angebotenen Preis. In Prozent ausgedrückt enthält die ‚Einfache Richtwertmethode‘ – immer – eine verlautbarte Gewichtung des Preises und der Leistung von je 50 % (vgl. (Opitz in: Beck`scher Vergaberechtskommentar, Bd. 1, 4. Aufl., § 127 GWB, Rn. 146). Andere Gewichtungen sind mit dieser Formel nicht umsetzbar (Delcuvé in: Müller-Wrede, GWB, 2. Aufl., § 127 GWB, Rn. 64).“
Aber ist es mathematisch überhaupt richtig, dass die Einfache Richtwertmethode immer ein Verhältnis von Leistung und Preis von je 50 % aufweist?
Beispielrechnung
Es liegen keine Informationen vor, wie viele Angebote und mit welchen Angaben eingegangen sind. Für die folgenden Überlegungen gehen wir daher einfach von nachstehendem Beispiel aus.
Auf der Leistungsseite sollen maximal 100 Wertungspunkte erreichbar sein. Es werden 4 Angebote mit folgenden Werten (nach Auswertung durch die Vergabestelle) betrachtet:
| Angebot | A | B | C | D |
| Leistungskennzahl L | 90 | 80 | 62 | 37 |
| Wertungspreis P | 730 € | 640 € | 550 € | 450 € |
Einen Grund, die Angemessenheit der Preise aufzuklären, gibt es in diesem Beispiel nicht, da die Aufgreifschwelle von 20 % nicht erreicht wird. (Die Wertungspreise der Angebote von C und D liegen 18,2 % auseinander. Und Angebot D ist hier auch in keinem Szenario ein Zuschlagskandidat, so dass sich die Frage der Preisaufklärung für Angebot D gar nicht stellen würde.)
Die Wertungsformel für die Einfache Richtwertmethode lautet für ein Angebot A:
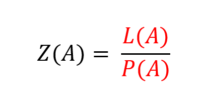
Somit ergibt sich gemäß o.g. Formel folgendes Wertungsergebnis:
| Angebot | A | B | C | D |
| Leistungskennzahl L | 90 | 80 | 62 | 37 |
| Wertungspreis P | 730 € | 640 € | 550 € | 450 € |
| Z (Einfache Richtwertmethode) | 0,1233 | 0,1250 | 0,1127 | 0,0822 |
Das Angebot B hat mit dem Wert 0,1250 hat die höchste Zuschlagskennzahl und erhält den Zuschlag.
Andere Wertungsformeln
Von der UfAB-II Formel gibt es verschiedene Ausprägungen. Für das Beispiel verwenden wir folgende Formel mit der Gewichtung von je 50 % für Leistung und Preis:
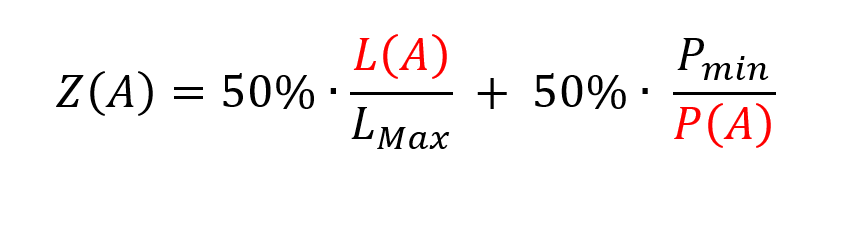
LMax ist dabei die maximal erreichbare Punktzahl, in unserem Beispiel also LMax = 100.
Pmin ist der niedrigste Preis aller wertungsfähigen Angebote, hier also der Preis von Angebot D und somit Pmin = 450.
Für die Auswertung mit der UfAB-II Formel ergibt sich folgendes Bild:
| Angebot | A | B | C | D |
| Leistungskennzahl L | 90 | 80 | 62 | 37 |
| Wertungspreis P | 730 € | 640 € | 550 € | 450 € |
| Z (UfAB-II Formel) | 0,7582 | 0,7516 | 0,7191 | 0,6850 |
Jetzt hat allerdings Angebot A trotz einer Preisgewichtung von 50 % die höchste Zuschlagskennzahl und erhält den Zuschlag.
Weiter betrachten wir auch noch die (einseitige) Interpolationsmethode (siehe hierzu Vergabeblog.de vom 07/07/2015, Nr. 22924). Hier werden die Preispunkte folgendermaßen bestimmt:
Das Angebot mit dem niedrigsten Wertungspreis (hier: Angebot D) erhält die volle Punktzahl. Ein fiktives Angebot mit einem fiktiv doppelt so hohem Wertungspreis (also 2x 450 € = 900 €) erhält 0 Preispunkte. Für alle anderen Angebote (hier: A, B und C) berechnen sich die Preispunkte durch lineare Interpolation.
Für die Zuschlagsformel der Interpolationsmethode gibt es verschiedene Darstellungen, die aber immer zum selben Zuschlagsergebnis führen. Die mathematisch ästhetischste Form lautet:
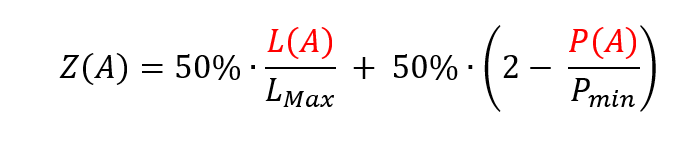
Damit ergibt sich folgende Auswertung:
| Angebot | A | B | C | D |
| Leistungskennzahl L | 90 | 80 | 62 | 37 |
| Wertungspreis P | 730 € | 640 € | 550 € | 450 € |
| Z (Interpolationsmethode) | 0,6389 | 0,6889 | 0,6989 | 0,6850 |
In diesem Fall hat trotz einer Preisgewichtung von 50 % nun Angebot C die höchste Zuschlagskennzahl und erhält den Zuschlag.
Rechthaberei
Hier nochmal die Auswertungen bei einer Preisgewichtung von 50 % im Vergleich. Wie man sieht, kommt jede Formel zu einem anderen Zuschlagsergebnis:
| Angebot | A | B | C | D |
| Leistungskennzahl L | 90 | 80 | 62 | 37 |
| Wertungspreis P | 730 € | 640 € | 550 € | 450 € |
| Z (Einfache Richtwertmethode) | 0,1233 | 0,1250 | 0,1127 | 0,0822 |
| Z (UfAB-II Formel) | 0,7582 | 0,7516 | 0,7191 | 0,6850 |
| Z (Interpolationsmethode) | 0,6389 | 0,6889 | 0,6989 | 0,6850 |
Falls die Einfache Richtwertmethode tatsächlich eine Gewichtung des Preises von 50 % umsetzen würde, welche Gewichtungen setzen dann die UfAB-II Formel und die Interpolationsmethode um? Erhält bei der UfAB-II Formel vielleicht die Leistung eine höhere Gewichtung als die in der Formel angegebenen 50 %? Und erhält vielleicht bei der Interpolationsmethode der Preis ein höheres Gewicht als die angegebenen 50 %?
Oder ist es gar so, dass in Wirklichkeit die UfAB II Formel die korrekte 50 %-Gewichtung umsetzt und damit sowohl die Interpolationsmethode als auch die Einfache Richtwertmethode gerade keine 50 %-Gewichtung umsetzen?
Oder kommt es noch viel schlimmer, und keine der drei vorgestellten Formeln setzt eine 50 %-Gewichtung korrekt um?
Wie müsste denn (die eine) Formel lauten, welche die 50 %-Gewichtung korrekt umsetzt?
Oder gibt es am Ende gar keine 50 %-Gewichtung? Sind diese Pseudoprozentangaben vielleicht zuletzt nur beliebige Formelparameter, die dem Leser (also den interessierten Marktteilnehmern, den Bietern und den Vergabekammern) eine Scheingewichtung vorgaukeln, aber eine entsprechende reale Gewichtung gar nicht umsetzen?
Aus mathematischer Sicht
| Tl;dr: Ein veröffentlichter angeblicher mathematischer Beweis der Aussage, dass die Einfache Richtwertmethode immer eine Gewichtung von 50 % aufweist, ist falsch. |
In Vergabe Navigator 1/18 stellte Ferber im Artikel „Mehr Schein als Sein. Die Gewichtung von Leistung und Preis“ einen angeblichen mathematischen Beweis vor, demzufolge
„die einfache Richtwertmethode mit der Zuschlagsformel Z (L, P) = L/P folglich immer eine feste Gewichtung von Leistungspunkten zu Angebotspreis von 50 % x 50 % besitzt.“
Hinweis: Ferber bezeichnet dort mit „Angebotspreis“ die Kennzahl, die wir hier – analog zur UfAB 2018 – als „Wertungspreis“ bezeichnen.
Denn, so Ferber, läge eine Gewichtung der Leistungspunkte und des Angebotspreises von 50 % / 50 % (genau?) dann vor, falls Z(L,P) = Z(α⋅L,α⋅P) für α > 0.
Die Grundidee ist also, dass eine 50 % Gewichtung dann vorliegen würde, wenn man zwei Angebote miteinander vergleicht, bei der das zweite Angebot um den Faktor α mehr Leistung enthält, aber dafür auch – ebenfalls um den Faktor α – mehr kostet. Diese beiden Angebote erhalten immer dieselbe Zuschlagskennzahl Z. Wenn also einer Leistungserhöhung (bzw. -reduzierung) eine entsprechende Preiserhöhung (bzw. -reduzierung) gegenübersteht (also beides mal um denselben Faktor α), ohne dass sich dadurch die Zuschlagskennzahl Z verändert, dann wäre das laut Ferber zumindest hinreichend, wenn nicht sogar gleichbedeutend für eine 50 %-Gewichtung.
Wir wollen diese Aussage als die „α-Bedingung“ bezeichnen.
In der Mathematik sind zwei Aussagen A und B dann „äquivalent“ (also gleichbedeutend), wenn die Aussagen gegenseitig „hinreichend“ und „notwendig“ sind.
Eine Aussage A ist für die Aussage B dann hinreichend, wenn B gelten muss, sobald A gilt. B folgt also aus A. Wenn A wahr ist, dann muss auch B wahr sein.
Eine Aussage A ist für die Aussage B dann notwendig, dass B nur dann wahr sein kann, wenn auch A wahr ist. Wenn A nicht wahr ist, dann kann und darf auch B nicht wahr sein. A folgt also aus B.
In mathematischer Notation:
A ist hinreichend für B: A ⇒ B
A ist notwendig für B: ¬A ⇒ ¬B
Das Zeichen „¬“ ist die ist die Negation und steht somit für das Wort „nicht“.
Tatsächlich sind die Bezeichnungen „notwendig“ und „hinreichend“ in der Mathematik das jeweilige Gegenteil voneinander. Denn statt ¬A ⇒ ¬B kann man auch A ⇐ B schreiben. Denn wenn B gilt, dann muss auch A gelten, da A ja notwendig für B ist. Falls also A nicht gelten sollte, dann kann auch B nicht gelten. Somit ist aber B eben auch hinreichend für A.
Und wenn sowohl A ⇒ B als auch A ⇐ B gelten, dann ist A ⇔ B. Also sind dann die Aussagen A und B äquivalent bzw. gleichbedeutend.
Schauen wir uns nach dieser kurzen Reminiszenz an die höhere Schulmathematik also den angeblichen Beweis von Ferber an.
Ohne Schwierigkeit kann man erkennen, dass die Einfache Richtwertmethode die α-Bedingung erfüllt. Denn
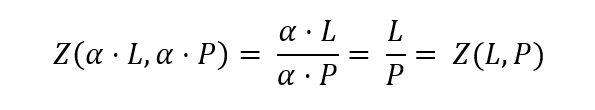
Aber ist damit auch bewiesen, dass die Einfache Richtwertmethode eine Gewichtung von 50 % aufweist?
Die Antwort ist nein. Denn die α-Bedingung ist nicht äquivalent zu der 50 %-Aussage. Die α-Bedingung ist nämlich nicht hinreichend für die 50 %-Aussage.
Für den Beweis des Nichthinreichens der α-Bedingung für die 50 %-Aussage genügt es bereits, wenn wir auch nur eine Zuschlagsformel finden würden, welche die α-Bedingung erfüllt, aber keine 50 %-Gewichtung aufweist.
Die simpelste Formel hierfür ist Z (L, P) = 1.
Diese Zuschlagsformel bewertet also jedes beliebige Angebot (unabhängig von L und P) immer mit dem Wert 1, unabhängig von Leistung und Preis des Angebots. Das mag zwar unter dem Gesichtspunkt der Vergabe eine unsinnige, weil für eine Zuschlagsentscheidung komplett ungeeignete Formel sein, aber aus mathematischer Sicht handelt es sich um eine völlig valide Zuschlagsformel, die geeignet ist, den gewünschten Beweis zu erbringen.
Man kann nun sehr leicht erkennen, dass die Zuschlagsformel Z (L, P) = 1 zwar die α-Bedingung erfüllt, aber sicherlich keine 50 %-Gewichtung umsetzt.
N.B. Eine andere, semantisch weniger sinnlose Zuschlagsformel, welche die α-Bedingung erfüllt, aber keine 50 %-Gewichtung umsetzt, ist Z (L, P) = L/(2P). Hier wird die Leistung also ins Verhältnis zum doppelten Preis gesetzt.
Aber wäre die α-Bedingung denn wenigstens notwendig für die 50 %-Aussage? Falls dem so wäre, dann würden aber weder die UfAB-II Formel noch die Interpolationsmethode die 50 %-Aussage erfüllen. Das würde bedeuten, dass man dann weder mit der UfAB-II Formel noch mit der Interpolationsmethode eine 50 %-Gewichtung herstellen könnte.
Denn man sieht bereits anhand des obigen Beispiels, dass weder die UfAB-II Formel noch die Interpolationsmethode die α-Bedingung erfüllen.
Sehen wir uns dazu stichprobenweise einige Beispiele an (die gesamte Gegenüberstellung kann beim Autor angefragt werden):
Gehen wir zunächst von α = 90 % (Abschlag von 10 % auf Leistung und Preis) aus. Das heißt, sowohl Leistung und Preis werden mit 90 % angesetzt. Für das Angebot A ergeben sich damit folgende Werte:
| ohne α | α= 90 % | |
| Angebot | A | A |
| Leistungskennzahl L | 90 | 81 |
| Wertungspreis P | 730 € | 657 € |
| Z (Einfache Richtwertmethode) | 0,1233 | 0,1233 |
| Z (UfAB-II Formel) | 0,7582 | 0,7475 |
| Z (Interpolationsmethode) | 0,6389 | 0,6750 |
Der gewünschte identische Wert ergibt sich also nur für die Einfache Richtwertmethode, aber nicht für die UfAB-II Formel oder die Interpolationsmethode.
Gehen wir umgekehrt von 10 % Aufschlag auf Leistung und Preis aus, also α= 110 %
| ohne α | α= 110 % | |
| Angebot | A | A |
| Leistungskennzahl L | 90 | 99 |
| Wertungspreis P | 730 € | 803 € |
| Z (Einfache Richtwertmethode) | 0,1233 | 0,1233 |
| Z (UfAB-II Formel) | 0,7582 | 0,7752 |
| Z (Interpolationsmethode) | 0,6389 | 0,6028 |
Auch bei einem Aufschlag von 10 % dasselbe Bild: Der gewünschte identische Wert ergibt sich somit nur für die Einfache Richtwertmethode, aber nicht für die UfAB-II Formel oder die Interpolationsmethode.
Die Berechnung der weiteren Werte für die restlichen Angebotsbeispiele werden dem Leser zur Übung überlassen oder können beim Autor angefordert werden.
Diejenigen besonders interessierten Leser, die das Thema tiefer untersuchen wollen, sollen auf den Umstand hingewiesen werden, dass die UfAB-II Formel und die Interpolationsmethode hier ein unterschiedliches Verhalten – zumindest in Bezug von Angebot A – aufweisen:
Denn eine Preis- und Leistungsreduzierung um 10 % (α=90 %) führt bei der UfAB-II Methode zu einer niedrigen Zuschlagskennzahl, aber bei der Interpolationsmethode zu einer höheren Zuschlagskennzahl.
Genau umgekehrt verhält es sich bei einer Erhöhung von Leistung und Preis um 10 % (α=110 %). Jetzt erhöht sich die Zuschlagskennzahl der UfAB-II Formel und die Zuschlagskennzahl der Interpolationsmethode reduziert sich. Dieses seltsame und gegenläufige Verhalten der beiden Formeln wurde bereits in Vergabeblog.de vom 30/01/2020, Nr. 43122 angerissen.
Die α-Bedingung ist bereits schon nicht bei den beispielhaften Angebotswerten erfüllt. Umso weniger kann dann die α-Bedingung für die UfAB-II Formel oder die Interpolationsmethode grundsätzlich erfüllt sein. Wäre die α-Bedingung also eine notwendige Voraussetzung für die 50 %-Aussage, dann könnten diese beiden Methoden (UfAB-II Formel oder Interpolationsmethode) zumindest bei einer gewünschten 50 %-Gewichtung nicht angewendet werden. Und übrigens auch nicht die Mittelwert- oder die Median- oder die Referenzwertmethode, die nämlich alle die α-Bedingung genauso wenig erfüllen.
So kommt es anders als man denkt
Ferber bemüht sich erstmals in der Literatur, eine Definition dafür zu geben, was eine Gewichtung zwischen Leistung und Preis bedeuten soll. Laut dieser Festlegung bedeutet es, dass eine Leistungsanpassung um dem Faktor α in ein gewichtetes Verhältnis einer Preisanpassung ebenfalls um den Faktor α gesetzt wird. Im Falle einer 50 % zu 50 % Gewichtung bedeutet das also, dass eine Leistungsanpassung um dem Faktor α und eine Preisanpassung um dem Faktor α zu einer unveränderten Zuschlagskennzahl führt.
Dann allerdings würden weder die UfAB-II Formel noch die Interpolationsmethode zur Gewichtung in einem Vergabeverfahren eingesetzt werden können, denn diese Formeln würden gerade die Ferber-Definition nicht erfüllen und niemals eine 50 %-Gewichtung umsetzen können. Diese Konsequenz hatte Ferber allerdings bestimmt nicht so beabsichtigt.
Somit wird eine andere Definition des Gewichtungsbegriffs benötigt. Diese liegt bis heute nicht vor.
Immerhin definiert aber die Rechtsnorm §127 GWB, dass sich die Wirtschaftlichkeit aus dem besten Preis-Leistungsverhältnis bestimmt. Und für das Preis-Leistungsverhältnis liegt aus der Betriebswirtschaft eine Definition vor, nämlich der Quotient aus Leistung und Preis. Und diese Definition wird von der Einfachen Richtwertmethode semantisch zutreffend und mathematisch korrekt umgesetzt. Allerdings findet sich da eben keinerlei Hinweis oder Möglichkeit auf eine etwaige Gewichtung zwischen Leistung und Preis.
Die falsche Frage?
Wenn wir mathematisch nicht einmal beweisen können, ob die Einfache Richtwertmethode die 50 % Gewichtung umsetzt, müssen wir uns vielleicht mal fragen, was die Gewichtung des Preises gegenüber der Leistung überhaupt bedeutet.
Zunächst bildet die Einfache Richtwertmethode das Preis-Leistungsverhältnis ab. Es handelt also schlicht um den Quotienten Z = L/P.
Kennen wir denn noch andere Quotienten, die uns regelmäßig in der Lebensrealität begegnen?
Ja klar, zum Beispiel im Auto das Stundenkilometerverhältnis: v = s/t. Das ist also die Geschwindigkeit v, denn die berechnet sich als der Quotient aus der Strecke s und der Fahrzeit t. Haben wir uns da schonmal gefragt, ob die km mit 50 % Gewichtung in die Berechnung eingehen? Oder gar die Fahrzeit (Stunden) mit 50 %? Was würde eine Aussage bedeuten, dass man für das optimale Stundenkilometerverhältnis gerne die Fahrzeit mit höherer Gewichtung als die Strecke berücksichtigen möchte? Unsinnig, oder?
In den USA wird die Geschwindigkeit in „mph“, also „miles per hour“ statt km/h berechnet. Eine Meile entspricht in etwa 1,6 km. Heißt das, dass die Amerikaner die Fahrstrecke mit 60 % mehr in die Geschwindigkeitsberechnung einbeziehen als die Deutschen? Gerade dieses Beispiel zeigt, wie unsinnig es ist, eine Gewichtung in einen Quotienten hineinzuinterpretieren.
Oder ein anderes Beispiel: Der Vergaberechtsfachanwalt stellt Rechnungen auf Basis eines Stundensatzes, also dem Verhältnis von Euro/Stunden. Auch hier ist die Frage inhaltlich sinnlos, ob er dabei die Euros oder die Leistungsstunden höher gewichtet hätte.
Und noch ein ganz anderes Beispiel: Um herauszufinden, wer Fußballmeister wird, werden die Tore und Gegentore in Siege und Punkte umgerechnet und dann – ggf. unter Berücksichtigung der Tordifferenz – eine Rangfolge gebildet. Die Frage, mit welcher Gewichtung ein einzelnes Tor hier in die Rangfolgeentscheidung eingegangen ist, kann man nicht sinnhaft beantworten, oder?
All dies sind leicht erkennbar inhaltlich völlig unsinnige Fragen.
Fazit
Man kann nicht sagen, ob die Einfache Richtwertmethode eine Gewichtung von 50 % umsetzt. Alleine schon deswegen nicht, weil es andere Zuschlagsformeln gibt, die ebenfalls behaupten, die Gewichtung von 50 % korrekt umzusetzen, aber zu anderen Zuschlagsergebnissen führen. Welche dieser Formeln setzt dann also – falls es das überhaupt gäbe – die korrekte Gewichtung zwischen Leistung und Preis um?
Schon bereits die Frage, mit welcher Gewichtung der Preis oder die Leistung bei der Einfachen Richtwertmethode berücksichtigt wird, kann nicht gestellt werden, da man sie nicht sinnhaft beantworten kann.
Und weiter hat auch bislang noch niemand eine Definition gegeben, was die Gewichtung zwischen Leistung und Preis überhaupt bedeuten soll.
Ist der Beschluss der VK Lüneburg dann aber im Ergebnis zu beanstanden?
Nein, keineswegs, Denn völlig zutreffend ist ja, dass der Bieter alleine durch die Angaben in den Vergabeunterlagen – also dass als Wertungsmethode die Einfache Richtwertmethode verwendet wird – die genauen Informationen erhält, wie er sein Angebot auszurichten hat. Und zwar allemal besser als bei allen anderen Zuschlagsformeln, die eine Scheingewichtung zwischen Leistung und Preis vorgaukeln, aber im Endeffekt zu nicht vorhersehbaren Zufallsergebnissen führen können.
Daher ein Lob auf die Wertung mit dem echten Preis-Leistungsverhältnis, nämlich die Einfache Richtwertmethode. Zumindest solange sie nicht in einem Atemzug mit einer angeblichen 50 %-Gewichtung genannt wird.
Aufruf zur Faktencheck-Challenge (ein persönliches Wort des Autors)
Liebe Leserin, lieber Leser, es freut mich, wenn Sie sich mit meinem Beitrag auseinandersetzen und ich bin auf Ihre Reaktionen sowie gerne Ihre Widerlegungen meiner Argumente gespannt – hier unter dem Beitrag als Kommentar oder im Mitgliederbereich des DVNW, wo ich einen Thread zu diesem Beitrag eröffnet habe. Gerne können Sie auch eine E-Mail an redaktion@dvnw.de richten. Ich möchte Sie gerne zu einer Faktencheck-Challenge einladen: Den ersten Leser oder Leserin, die einen rechnerischen, mathematischen, logischen oder argumentativen Fehler in dem Aufsatz (Schreibfehler ausgenommen) findet, lade ich am Vorabend des DVNW Vergabetags 2024 zusammen mit einer Begleitperson seiner/ihrer Wahl zum Abendessen in Berlin ein. Die Reisekosten müsste der oder die Einreicher:in allerdings selber tragen.
Über Wolfgang Bartsch
Dipl.-Inform. (univ.) Wolfgang Bartsch ist Managing Consultant im Bereich Beschaffungsberatung bei der IABG mbH. Er berät öffentliche Auftraggeber und Bieter bei Vergabeverfahren, insbesondere bei Ausschreibungen von komplexen und technisch anspruchsvollen IT-Lösungen wie beispielsweise landesweite Behördennetze oder große Outsourcingvorhaben. Seit vielen Jahren untersucht er Zuschlagsformeln auf mathematische Schwächen und hat dazu unter anderem auch die UfAB Arbeitsgruppe beraten.







 (22 votes, average: 4,45 out of 5)
(22 votes, average: 4,45 out of 5)
Vielen Dank für Ihren Beitrag. Auf der Grundlage der drei gewählten Zuschlagsformeln:
Z 1 = L/P
Z 2 = 50 % * L(A) / L(Max) + 50 % * P(min) / P(A)
Z 3 = 50 % * L(A) / L(Max) + 50 % * (2-P(A) / P(Min))
und bei einer Annahme von L(max) = 500 und P(min) = 500 würde das beste denkbare Angebot (A1) mit einem Preis von L=500 und P=500 nach allen Ihren drei Berechnungsformeln den Zuschlagswert Z = 1,000 erreichen.
Z1 = 500/500 = 1/1 = 1
Z2 = 0,5*500/500+0,5*500/500 = 0,5+0,5 =1
Z3 = 0,5*500/500+0,5*(2-500/500) = 0,5+0,5*(2-1) = 1
Wenn die Angabe einer Gewichtung von 50% für den Preis und 50% für die Leistung darauf hindeuten soll, dass ein AG Preis und Leistung gleichwertig bei der Ermittlung des wirtschaftlichsten Angebots berücksichtigen möchte, müssten dann ein gleichgünstiges Angebot (A2) mit einer um 10% niedrigeren Leistungspunktzahl (L=450 und P =500) und ein gleichgutes Angebot (A3) mit einem um 10% höheren Preis (L=500 und P=550) jeweils den gleichen Zuschlagswert erreichen?
Z1(A2) = 450/500 = 0,900 (= -10,0%)
Z1(A3) = 500/550 = 0,909 (= -9,09%)
Z2(A2) = 0,5*450/500+0,5*500/500 = 0,450+0,500 = 0,950 (= -5,00%)
Z2(A3) = 0,5*500/500+0,5*500/550 = 0,500+0,454 = 0,954 (= -4,55%)
Z3(A2) = 0,5*450/500+0,5*(2-500/500) = 0,450+0,500 = 0,950 (= -5,00%)
Z3(A3) = 0,5*500/500+0,5*(2-550/500) = 0,500+0,450 = 0,950 (= -5,00%)
Käme danach ein Bieter bei der einfachen Richtwertmethode und der UfaB-II-Formel mit einer 10% niedrigeren Leistungspunktzahl schlechter weg, als ein Bieter mit einem 10% teureren Preis? Und würde allein die gewählte Interpolationsmethode (Z3) Leistung und Preis gleichwertig berücksichtigen (wobei nach aktuellem Diskussionsstand durch Mindestleistungspunktzahlen und Preisobergrenzen unerwünschte Effekte zu minimieren wären)?
Sehr geehrter Herr Nepp,
vielen Dank für Ihr inspirierendes Beispiel, welches eine nähere Betrachtung verdient.
Sie schlagen als Definition für die 50 %-Gewichtung vor, von einem Angebot A1 auszugehen und davon abgeleitet von einem zweiten Angebot A2, welches denselben Preis, aber x % weniger Leistung als A1 aufweist, und schließlich von einem dritten Angebot A3, welches zwar dieselbe Leistung wie Angebot A1, aber einen 10% höheren Preis aufweist. Und dann soll im Falle einer 50 %-Gewichtung die Zuschlagskennzahl von Angebot A2 und Angebot A3 gleich sein (und natürlich niedriger als die Zuschlagskennzahl von Angebot A1, auch wenn Sie das nicht explizit dazu gesagt hatten).
Für Ihr Rechenbeispiel legen Sie das „bestmögliche“ Angebot A1 zugrunde, also dasjenige mit der höchstmöglichen Leistungskennzahl (500) und gleichzeitig dem niedrigsten Preis (500) aller Angebote.
Anhand dieses Beispiels berechnen Sie, dass bei Anwendung der Einfachen Richtwertmethode (Z = L/P) die von Ihnen aufgestellte Bedingung nicht eingehalten wird. Und genauso gilt das für die Anwendung der UfAB-II Formel. Nur bei der Formel der (einseitigen) Interpolationsmethode ergibt sich rechnerisch, dass die Zuschlagskennzahl Z3 für die Angebote A2 und A3 identisch sind.
Zunächst ist festzuhalten, dass Ihre Angaben zumindest rechnerisch korrekt sind.
Erste Überlegung:
Sollte Ihre aufgestellte Bedingung aber tatsächlich gleichbedeutend mit einer 50 %-Gewichtung von Leistung und Preis sein, dann würde daraus folgen, dass weder die Einfache Richtwertmethode noch die UfAB-II-Methode eine 50 %-Gewichtung umsetzen. Nur welche Gewichtung setzen diese Formeln dann um?
Zweite Überlegung:
Ihre Bedingung für die 50 %-Gewichtung müsste ja für sämtliche Angebote gelten. Denn wenn die Bedingung nur für vereinzelte Angebote gelten würde, dann würde es sich nicht um eine allgemeingültige Festlegung handeln.
Schauen wir uns dazu einfach mal ein weiteres Angebot B1 (statt A1) an, welches auf der Leistungsseite 400 Punkte erhalten hat und einen Preis von 600 aufweist. L_Max ist ja weiterhin 500 Punkte und P_min weiterhin 500.
Für die Interpolationsmethode ergibt sich dann folgende Zuschlagskennzahl:
Z3(B1) = 50% x L/L_Max + 50% x (2 – P/P_min) = 50% x 400/500 + (2 – 600/500) = 0,80
Nun betrachten wir (analog zu Ihrer Darstellung) die Angebote B2 (10% weniger Leistungspunkte bei gleichem Preis wie B1) und B3 (10% höherer Preis bei gleicher Leistung wie B1)
Z3(B2) = 50% x 360/500 + (2 – 600/500) = 0,76 (-0,4 bzw. -5%)
Z3(B3) = 50% x 400/500 + (2 – 660/500) = 0,74 (-0,6 bzw. -7,5%)
Sie sehen also, dass Ihre Bedingung für die 50%-Gewichtung für die Angebote B1, B2 und B3 nicht gelten, da eben nicht dieselbe Zuschlagskennzahl für B2 und B3 herauskommen.
Tatsächlich kann man mathematisch zeigen, dass die Bedingung ausschließlich(!) für das bestmögliche Angebot A1 gilt, welches die maximale Leistungskennzahl und den niedrigsten Preis aufweist. Für alle anderen Angebote gilt diese Bedingung schon nicht mehr bei der Anwendung der Interpolationsmethode. Somit setzt auch die Interpolationsmethode die 50 %-Gewichtung nicht um, falls man die o.g. Bedingung als Definition der Gewichtung festlegen würde.
Zusammengefasst hat Ihr Kommentar meine These aus dem Artikel, dass es keine Gewichtung zwischen Leistung und Preis gibt – zumindest nicht für eine scheinbare 50 %-Gewichtung – zwar herausgefordert, aber letztlich nicht erschüttert.
Sehr geehrter Herr Bartsch,
vielen Dank für Ihre ausführliche Antwort.
Mein Vorschlag setzt – wie von Ihnen zutreffend angemerkt – stets voraus, dass die Angebote an einem hypothetischen Bestangebot (L_Max und P_Min) gemessen werden. Eine solche Prämisse für ein relatives „Gewichtungsverständnis“ scheint mir aber nicht per se ausgeschlossen. Auch die Berechnungsformeln selbst setzten mathematische Prämissen, mit dem Ziel, die normativen Vorgaben zu erfüllen.
Fraglich wäre daher, ob eine Gewichtungsangabe in den Vergabeunterlagen: „50% Preis und 50 % Leistung gemessen an der maximalen Leistungspunktzahl und der geringsten Preispunktzahl nach der Interpolationsmethode (Z=0,5*L/L_max+0,5*(2-P/P_min)“ hinreichend transparent wäre und den normativen Anforderungen genügen würde.
Wie sie zutreffend ausführen, muss das von Ihnen angeführte Beispiel zu abweichenden Z3-Ergebnissen führen, da die Angebote B2 und B3 in Relation zum hypothetischen Bestangebot mit L_Max und P_Min unterschiedlich weit entfernt sind. Das Angebot B2 hat eine gegenüber L_Max um 28 % niedrigere Leistungspunktzahl (500*0,8=400*0,9=500*0,72=360), wohingegen das Angebot B 3 einen gegenüber dem Bestpreis P_min um insgesamt 32 % (500*1,2=600*1,1=660) höheren Preis aufweist. Würde die Abweichung der Leistung des Angebotes B2 und des Preises des Angebotes B3 gleich weit von L_max und P_min entfernt sein (z.B. jeweils 30%, mit L(B2) = 500*1,3=650 und P(B3) = 500*0,7=350, wären B2 und B3 gegenüber B1 wiederum mit Z3(B2) = Z3 (B3) = 0,75 gleichwertig.
Es bleibt abzuwarten, wie sich die Diskussion in der Literatur, die Rechtsprechung und etwaige nationale bzw. europäische Gesetzgebung hierzu entwickeln.
Sehr geehrter Herr Nepp,
aufgrund der fehlenden Möglichkeit, in den Kommentaren Formatierungen vorzunehmen, wäre vielleicht einfacher, wenn Sie mir Ihre Kontaktdaten übermitteln. Dann können wir die Fragestellungen nämlich gerne direkt und viel besser vertiefen.
Die von Ihnen vorgeschlagene Definition der 50 %-Gewichtung würde man mathematisch so fassen:
Eine Zuschlagsformel Z(L; P) weist (genau?) dann eine 50 %-Gewichtung auf, wenn folgendes gilt:
Z((1 -ε) ⋅ L_Max; P_min) = Z(L_Max; (1 + ε) ⋅ P_min) für 0 < ε < 1.
Wir wollen diese Bedingung als ε-Bedingung bezeichnen.
Es ist völlig in Ordnung, eine solche Definition aufzustellen. Im zweiten Schritt müssen Sie aber noch nachweisen, dass es sich um eine _sinnvolle_ Definition handelt.
Und da bin ich aber anderer Auffassung.
Ähnlich wie die α-Bedingung (siehe oben) ist Ihre Definition schon nicht _hinreichend_. Denn es gibt auch eine andere Formel (als die einseitige Interpolationsmethode), die die ε-Bedingung zwar erfüllt, aber definitiv keine Gewichtung zwischen Leistung und Preis aufweist. Es ist dieselbe Zuschlagsformel Z(L; P) = 1, die ich auch im Artikel verwendet habe. Ob es weitere Formeln gibt, die die ε-Bedingung erfüllen, aber keine 50 %-Gewichtung aufweisen, müssten Sie noch untersuchen.
Aber ist die ε-Bedingung zumindest _notwendig_ für die 50 %-Gewichtung?
Denn wenn die ε-Bedingung _notwendig_ für die 50 %-Gewichtung wäre, dann können weder die Einfache Richtwertmethode noch die UfAB-II Formel und schon gar nicht andere Zuschlagsformeln eine 50 %-Gewichtung umsetzen.
Anders gesagt: Dann sind Sie in derselben Situation wie Herr Ferber bzgl. der α-Bedingung, die ja ebenfalls zur Folge hat, dass keine der bekannten Zuschlagsformeln mit einer Scheingewichtung des Preises eine 50 %-Gewichtung umsetzen könnte. Sie beide müssten jetzt also noch sämtliche andere Formelerfinder davon überzeugen, dass deren Formeln nicht funktionieren, solange sie die α- bzw. ε-Bedingung nicht einhalten (was die anderen Zuschlagsformeln nicht tun). (Und da sich die α-Bedingung und die ε-Bedingung gegenseitig ausschließen, müssten Sie sich zunächst mit Herrn Ferber einigen, welche der Bedingungen gelten soll…)
Was mich ebenfalls an der ε-Bedingung stört, ist, dass diese nur für das seltenste denkbare Angebot gilt, nämlich dasjenige mit dem niedrigsten Preis P_min und der maximal erreichbaren Leistungskennzahl L_Max. Außer bei Ausschreibungen, bei denen am Ende nur ein einziges wertbares Angebot übriggeblieben ist, habe ich in meiner Vergabepraxis noch nie so ein Angebot gesehen. Und falls es tatsächlich mal so ein Angebot geben würde, dann wäre bereits jede Scheingewichtung des Preises völlig obsolet, weil man ja auf jeden Fall dieses seltenste aller Angebote bezuschlagen würde, egal welche Scheingewichtung des Preises man zugrunde legen würde.
Um das nochmal an einer Metapher verdeutlichen:
Stellen Sie sich nur mal vor, Sie wollen einen Kompass nutzen. Der Kompass soll dabei eine Gewichtung von 50% zwischen den Himmelsrichtungen Nord und Süd aufweisen. Als Definition der 50 %-Nord-Süd-Gewichtung soll folgendes gelten:
„Sie folgen dem Kompass in Richtung Norden für 100 Meter. Anschließend folgen Sie dem Kompass in Richtung Westen für 100 Meter. Dann folgen Sie dem Kompass in Richtung Süden für 100 Meter. Wenn Sie sich dann wieder am Ausgangspunkt befinden, dann weist der Kompass eine Gewichtung von jeweils 50 % für die Himmelsrichtungen Nord und Süd auf.“
Tatsächlich gibt es (sehr seltene) Orte, für die das tatsächlich möglich ist; beispielsweise der Südpol.
Aber würden Sie eine solche Definition einer Gewichtung überhaupt akzeptieren, wenn die nur am Südpol (und an sehr wenigen weiteren Orten) gelten würde, und sonst nie?
Vielleicht argumentieren Sie ja dann, dass das seltenste denkbare Angebot (L_Max, P_min) nur als Bezugspunkt für die Definition dienen würde (analog dem Südpol als Bezugspunkt für den Kompass).
Da muss ich Ihnen aber erwidern, dass die Bieter so nicht „ticken“. Denn die Bieter denken (um in Ihrem Beispiel zu bleiben) eher so:
Wenn ich für mein eigenes Angebot die Leistung um den Faktor (1+ε) erhöhe, bekomme ich dann genauso viele Punkte (bei einer 50 %-Scheingewichtung), wie wenn ich den Preis um den Faktor (1-ε) reduziere? Bzw. umgekehrt, so dass sich eine entsprechende Leistungsreduzierung und Preiserhöhung entsprechen?
Und kein Bieter wird realistischerweise davon ausgehen, dass sein eigenes Angebot sowohl den niedrigsten Preis als auch die maximal mögliche Leistung aufweist.
Anders gesagt: Die ε-Bedingung müsste eigentlich für beliebige Angebotswerte L und P gelten, nicht nur für das seltenste denkbare Angebot. Aber das tut sie nicht (siehe meine erste Erwiderung und Ihre Bestätigung in Ihrer Erwiderung).
Im Übrigen kennen die Bieter ja zum Zeitpunkt der Angebotserstellung P_min noch nicht. Somit hätten die Bieter auch gar keine Chance, Überlegungen im Sinne Ihrer Erwiderung durchzuführen.
Daher halte ich die ε-Bedingung für keine geeignete Definition einer 50 %-Gewichtung zwischen Leistung und Preis.
P.S.: Übrigens kann man die von Ihnen vorgeschlagene Zuschlagsformel Z=0,5*L/L_max+0,5*(2-P/P_min) ohne Beeinträchtigung der resultierenden Rangfolge der Angebote immer auch drastisch vereinfachen zu
Z(L; P) = L/L_Max – P/P_min
Mehrere Mitleser der juristischen Fraktion (und vielleicht auch andere Leser:innen) hatten mir zurück gemeldet, dass die im Artikel verwendeten (mathematischen) Begriffe „notwendig“ und „hinreichend“ sehr abstrakt wären.
Vielleicht ist hilfreich, wenn man es in juristische Begriffe übersetzt.
Die „Notwendigkeit“ einer Aussage oder Behauptung oder eines Sachverhalts entspricht in erster Näherung dem Begriff der „Zulässigkeit“ bei einem Nachprüfungsverfahren: Ist die entsprechende Voraussetzung (Aussage, Behauptung, Sachverhalt) nicht gegeben, dann geht das Vergabeverfahren auch negativ (für den Antragsteller) aus.
Zitat aus dem Artikel: A ist notwendig für B: ¬A ⇒ ¬B
(¬ liest man als „nicht“.)
Ist die Notwendigkeit (Aussage, Behauptung, Sachverhalt) jedoch gegeben, dann sagt das noch nichts über den Ausgang des Nachprüfungsverfahrens aus.
Sollte das Verfahren aber positiv (für den Antragsteller) ausgegangen sein, dann war die Zulässigkeit auch gegeben.
Mathematisch: B ⇒ A
Eine „hinreichende“ Aussage/Behauptung/Sachverhalt ist am ehesten mit der juristischen Begründetheit vergleichbar. Ist eine Aussage hinreichend, dann ist sie im juristischen Duktus begründet und führt (in der Regel) dazu, dass das Nachprüfungsverfahren (für den Antragsteller) positiv beschieden wird.
Zitat aus dem Artikel: A ist hinreichend für B: A ⇒ B
Ist das Nachprüfungsverfahren nicht positiv (für den Antragsteller) ausgegangen, dann waren seine Argumente eben nicht hinreichend.
Mathematisch: ¬B ⇒ ¬A
So, das war jetzt stark vereinfacht. Aber ich hoffe, die Begriffe „notwendig“ und „hinreichend“ sind jetzt etwas klarer. Etwaige juristische Unsauberkeiten bzw. Unschärfen bitte ich zu entschuldigen.